Intégrateur

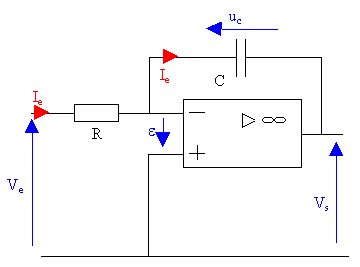
Figure N°7

1) Etude générale

a) Hypothèses de calcul.

Quelles sont les hypothèses utilisables pour l’étude de ce montage ?

b) Rappels sur le condensateur

On rappelle que pour le courant :

avec q quantité d’électricité qui traverse le conducteur. L’intensité du courant représente donc la quantité d’électricité par unité de temps.

On rappelle que pour le condensateur :

q = C u_c

avec q charge portée par une armature, C capacité du condensateur et u_c tension aux bornes du condensateur.

Donner l’expression de I_e en fonction de C et u_c.

c) Relation entre V_s et u_c

Donner la relation entre V_s et u_c.

d) Relation entre I_e et V_e.

Donner l’expression de I_e en fonction de V_e et R

e) Relation entre I_e et V_s

Donner l’expression de I_e en fonction de V_s et C.

f) Relation entre V_e et V_s

Donner l’expression de V_e en fonction de V_s, R et C.

2) Application numérique

On donne l’oscillogramme de V_e :

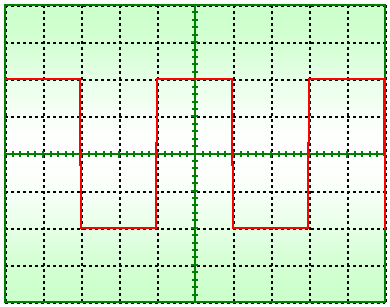
Sensibilité : 0,5V/div

Base de temps : 1ms/div.

a) Etude du signal

Donner la valeur de la demi-période du signal d’entrée.

Donner l’amplitude de V_e.

b) Calcul de RC

On donne R = 10 kΩ et C = 10 nF

Donner la valeur du produit RC.

c) Caractéristique de I_e

Pendant la première demi-période du signal d’entrée :

Donner la valeur de I_e pendant la première demi-période :

d) Expression de u_c pour 0 £ t £ T/2

Sachant que le courant est constant, quelle est l’allure de u_c(t) :

On définit la variation de la tension aux bornes du condensateur : Δu_c = u_c(t) – u_c0

Qui correspond à la variation de temps Δt = t – 0 = t.

On rappelle que I_e = C du_c/dt ce qui donne pour des variations finies I_e = C(Δu_c / Δt).

Cocher la bonne expression de Δu_c :

A partir de la réponse précédente, donner l’expression de u_c(t) en fonction de I_e, t, C et u_c0 :

Attention : pour alléger la notation, u_c(t) sera noté simplement u_c dans l'expression.

e) Application numérique

On admet que en t = 0 ms u_c(0) = u_c0 = -10 V.

Pour 0 = t = T/2 donner l’expression numérique de u_c(t)

Attention : pour alléger la notation, u_c(t) sera noté simplement u_c dans l'expression.

f) Valeur de u_c pour t = T/2

Donner la valeur de u_c(T/2). On rappelle que T/2 = 2 ms.

g) Caractéristique de I_e

Pendant la deuxième demi-période du signal d’entrée :

Donner la valeur de I_e pendant la deuxième demi-période :

h) Expression de u_c pour T/2 = t = T

Sachant que le courant est constant, quelle est l’allure de u_c(t) :

Pour simplifier les calculs on fait un changement d’origine des temps. On fixe l’origine des temps à T/2. On note la nouvelle variable de temps t’. Donc t’ = t – T/2. Grâce à cette méthode on obtient comme précédemment avec la nouvelle variable :

i) Application numérique

On admet que en t’ = 0 ms u_c(0) = u_c0 = +10 V.

Pour 0 = t’ = T/2 donner l’expression numérique de u_c(t’)

Attention : pour alléger la notation, u_c(t') sera noté simplement u_c' dans l'expression.

j) Valeur de u_c pour t’ = T/2

On rappelle que en t’ = T/2, t = T.

Donner la valeur de u_c en t’ = T/2. On rappelle que T/2 = 2 ms.

k) Signal de sortie

On rappelle que V_s = -u_c et que l'étude réalisée jusqu'ici porte sur u_c.

Choisir le bon signal de sortie parmi les oscillogrammes suivants:

sensibilité : 5 V/div

Base de temps : 1 ms/div

Nos plus vifs remerciements à M^r Yvan Crévits qui nous a permis d'utiliser son cours.

Le GER de l'académie de Montpellier.

retour à la page d'accueil