Nombre complexes et régimes sinusoïdaux

Nombres complexes

A la tension sinusoïdale u(t), on peut associer un nombre complexe U tel que :

Module de U : | U | = U

Argument de U : arg( U ) = θ_u

En notation cartésienne : U = a + j b

avec a partie réelle de U et b partie imaginaire de U.

En notation polaire : U = [U, θ_u]

avec U module de U et θ_u argument de U.

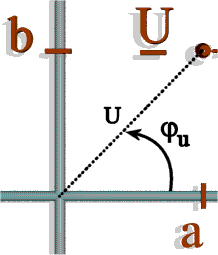
Représentation :

Remarque : j est le nombre complexe tel que

Polaire => cartésienne :

Cartésienne => polaire :

Exemple :

3 + j 4 = [ 5 ; 53,1 ° ]

Soient = [U₁, θ_u1] = a₁ + j b₁, = [U₂, θ_u2] = a₂ + j b₂ et U = [U, θ_u] = a + j b

Si U = +

Alors : a = a₁ + a₂ et b = b₁ + b₂

Donc U = (a₁ + a₂) + j (b₁ + b₂)

Si U = -

Alors : a = a₁ - a₂ et b = b₁ - b₂

Donc U = (a₁ - a₂) + j (b₁ - b₂)

Exemples :

( 3 + j 4 ) + ( 4 + j ) = 7 + j 5

( 3 + j 4 ) - ( 4 + j ) = -1 + j 3

ATTENTION :

U ≠ [ U₁ + U₂ ; θ_u1 + θ_u2]

U ≠ [ U₁ - U₂ ; θ_u1 - θ_u2]

Soient = [U₁, θ_u1] = a₁ + j b₁, = [U₂, θ_u2] = a₂ + j b₂ et U = [U, θ_u] = a + j b

Si U = x

Alors : U = U₁ x U₂ et θ_u = θ_u1 + θ_u2

Donc U =

Si U =

Alors : U = et θ_u = θ_u1 - θ_u2

Donc U =

Exemples :

[ 5 ; 35 °] x [ 2 ; 15 ° ] = [ 10 ; 50 °]

[ 5 ; 35 °] / [ 2 ; 15 ° ] = [ 2,5 ; 20 °]

ATTENTION :

U ≠ (a₁ x a₂) + j (b₁ x b₂)

U ≠ + j

Autre formule :

U = (a₁ + j b₁) (a₂ + j b₂) = a₁ a₂ + j a₁ b₂ + j b₁ a₂ + j j b₁ b₂ = a₁ a₂ + j a₁ b₂ + j b₁ a₂ - b₁ b₂

U = (a₁ a₂ - b₁ b₂) + j(a₁ b₂ + b₁ a₂)

Exemple :

( 3 + j 4 ) x ( 4 + j ) = (3 x 4 - 4 x 1) + j(3 x 1 + 4 x 4) = 8 + j 19