On note y(t) la valeur instantanée d'une grandeur sinusoïdale. y(t) représente la valeur que prend la grandeur y à l'instant t.
Pour une grandeur sinusoïdale on peut écrire :
Grandeurs caractéristiques :
Y est la valeur efficace telle que 
où 
représente la valeur maximale de y(t).
ω est la pulsation (en rad.s-1) telle que 
où T est la période (en s) et 
est la fréquence (en Hz)
φ est la phase à l'origine (en rad).
|
Remarque :
.A chaque instant t, les lois fondamentales de l'électrocinétique sont valables (lois des nœuds, des mailles et d'Ohm).
Lors du maniement de ces grandeurs, il faut tenir compte à la fois de l'amplitude des signaux et de leur différence de phase. Ainsi deux tensions sinusoïdales de même amplitude (1V par exemple) peuvent donner par addition une grandeur sinusoïdale d'amplitude de 0 à 2 suivant la différence de phase qui existe entre elles.
Exemple 1 :
|
|
|
Exemple 2 :
|
|
|
|
Représentations d'une grandeur sinusoïdale
A toute grandeur sinusoïdale, peut-être associé un vecteur tournant :
|
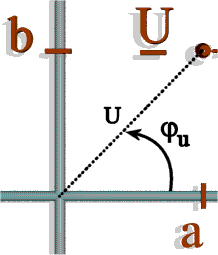
Le vecteur de Fresnel 
associé à une tension 
est un vecteur dont la norme est la valeur efficace de u(t) et faisant un angle φu avec l'axe des abscisses.
|
|
A toute grandeur sinusoïdale, peut-être associé un nombre complexe :
Le nombre complexe U associé à une tension est un nombre dont le module est la valeur efficace de u(t) et l'argument est φu.
|
|
On rappelle qu'un nombre complexe peut être donné sous forme polaire ou sous forme cartésienne :
U = [U ; φu] = a + j b.
Toute opération entre des grandeurs sinusoïdales peut-être ramenée à une opération entre vecteurs de Fresnel ou nombres complexes associées à ces grandeurs sinusoïdales.